| Radiation by the Thermodynamic Equilibrium |
Radiation by the Thermodynamic Equilibrium
Òhe theory becomes much easier if the plasma is considered as the closed ensemble. In this case the plasma does not share the energy with the outer space. The energy exchange is possible between the particles of the plasma itself as a result of their interaction. After such an exchange after a while, which value dependes on the concentration of the particles and their speeds, the equilibrium is established by which the average kinetic energy of forward motion of atoms, ions and electrons will be equal and it will be 3/2 kÒ.
Such plasma is called isothermic or Bolzman radiator. The isolated homogeneous plasma which is in thermodynamic equilibrium by the temperature Òand which consists of ideal monoatomic gas can be described with the following 5 correlations.
1. Pressure ð in the plasma is calculated from the equation of condition:
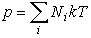 . (1)
where Nà, Nion, Nå - concentrations (number of particles in the volume unit) of atoms, ions and electrons respectively,
k - Bolzman constant.
2. Distribution of particles of any kind i acc. to the speeds
v
is expressed by Maxvell function:
Ni(n )=4p Ni(Mi/2p kT)
3/2 exp(-Mi n2 / 2kT), (2)
where Mi is the mass of particles;
Ni(n) - number of particles (concentration), having speeds from n
up to
n+dn;
Ni
is a concentration, which is equal to:
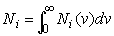 . (3)
3. The number of atoms and ions which are in arbitrary excited condition k
(occupying of the condition k
), is defined by the Bolzman formula:
Nk=N0 (gk/g0
) exp(-Ek/kT) = N(gk /U) exp(-Ek/kT). (4)
Here N0 is the occupying of the main state;
g0 is a statistic weight of this condition; gk is a statistic weight of the excited state; Ek is the energy of excited state, counted from the main level. Amounts on the conditions of atoms and ions:
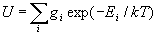 .(5)
4. In case of a single gas ionization the concentrations of atoms, ions and electrons are connected with each other with the Sah formula:
NeNNeNèîí/Na=
[2(2p me)3/2/h3](kT)3/2 [Uèîí(T)/Ua(T)]exp(-Eè/kT),
(6)
Where me is the mass of an electron; Ei is the energy of ionization; Uion(T) and Ua(T)are amounts on conditions of ions and atoms; g = 2 is a statistic weight of electrons.
5. The spectral brightness of plasma radiation b0lT
in the interval of waves lengths from l up to l + dl is calculated on Plank formula:
blT0dl =[2hc2/l5]
/ [exp(hc/l kT)-1] dl . (7)
I
n the plasma described with correlations (1) - (7) the conditions of detailed equilibrium are realized. They are in the fact, that optic and percussive (striking) processes of excitement and deexcitement of each level in the volume unit, occuring in the time unit are balanced. The radiation occuring in a volume unit of such a plasma is fully absorbed in the volume unit: the plasma is optically dense for such radiation.
In the reality it is much more difficult to answer Plank formula because the radiation process into the outer space by itself is a violation of equilibrium. However there are sources of radiation in which the conditions are close to the conditions of thermodynamic equilibrium and the radiation is calculated on Plank formula in the wide area of spectrum.
|
