Основная задачи осуществления УТС – нагрев DT-плазмы до температур в сотни миллионов градусов и изоляция ее от стенок реактора на время протекания термоядерных реакций.

Степень сохранения высокотемпературной плазмы в реакторе принято характеризовать временем сохранения энергии плазмы τ_E, показывающий, как долго в ней поддерживаются условия для протекания ТЯ-реакции по температуре и плотности.

Основные термоядерные реакции

Термоядерная энергетика основана на выделении энергии при реакциях синтеза. Наиболее важными являются следующие реакции синтеза:

Запасы дейтерия на Земле фактически неисчерпаемы. В океане содержится 4,6•10³ тонн воды, а в 1 тонне воды содержится 33 г дейтерия. По энергии 1 литр воды эквивалентен 260 литрам бензина.

По-видимому, первой будет освоена для практического применения реакция дейтерия с тритием (D-T реакция), для достижения которой требуются меньшие значения как температуры плазмы, так и времени ее удержания. В этом случае лимитирующим фактором являются ресурсы не дейтерия, а лития. Поскольку трития в природе не существует, то его получают при облучении ядер лития нейтронами по реакциям:

Это можно осуществить в атомном реакторе или в самом термоядерном реакторе, окружив его оболочкой из лития и воспользовавшись нейтронами от термоядерных реакций. Запасов же лития как в земной коре (1900 Q), так и особенно в воде (2,75•10⁶ Q) достаточно много, их хватит на многие тысячи лет.

Влияние электрического поля

Чтобы сблизить два ядра с зарядами Z₁ и Z₂ на расстояние r, надо согласно закону Кулона затратить энергию для преодоления силы электрического отталкивания:

Для ядер водорода (Z₁ = Z₂ = 1) и r = 10^-12 см E = 0,15 МэВ. На таком расстоянии ядра вступают в реакцию синтеза. Трудности преодоления кулоновского отталкивания возрастают по мере увеличения заряда ядра Z, что требует все большей энергии сталкивающихся ядер, а значит, более высокой температуры плазмы. По этой причине в промышленных термоядерных реакторах можно использовать только самые легкие ядра – изотопы водорода и гелия.

Скорость протекания ядерной реакции

Для преодоления кулоновского барьера ядро надо разогнать и направить на ядро-мишень. Для простоты представим оба ядра в виде твердых шариков радиусами r₁ и r₂, тогда столкновение произойдет, если расстояние между ядрами окажется в какой-то момент меньше, чем r₁+r₂.

Теперь представим налетающее ядро в виде "диска" радиуса R=r₁+r₂, а ядра мишени в виде точек и будем считать, что реакция происходит каждый раз, когда ядро мишени оказывается в пределах диска. Площадь такого диска назовем сечением реакции синтеза. Площадь сечения диска, естественно, зависит от скорости налетающего ядра и свойств ядра-мишени.

Чтобы рассчитать скорость реакции в рамках такой простой модели, вводят понятие эффективного сечения реакции и обозначают его буквой σ. Значения эффективных сечений могут быть определены экспериментально. На рис. 1 приведены экспериментальные значения эффективных сечений реакций синтеза для D+D, D+T и He³+D реакций в зависимости от энергии налетающего ядра.

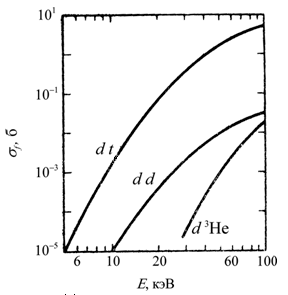
Рис.1

Из рис.1 видно, что максимальное сечение наиболее выгодной для УТС DT-реакции достигается при энергии налетающих частиц 50-100 кэВ. За счет того, что в плазме существует распределение частиц по скоростям, т.е. присутствуют ионы как с большей, так и меньшей энергией, термоядерные реакции могут происходить при более низкой температуре. На рис. 2 приведены результаты усреднения зависимостей σ(E) с учетом максвелловского распределения частиц по энергиям. Высокоэнергетический "хвост" распределения частиц по энергии позволяет снизить требование по температуре плазмы почти в 10 раз, сделав их трудными, но вполне достижимыми.

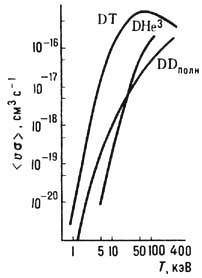
Рис.2

Условия работы реактора с положительным выходом энергии

Наиболее выгодной реакцией синтезадля энергетического реактора является реакция

Выделяющаяся в одном акте синтеза энергия делится между продуктами реакции в соответствии с их массами: 3,5 МэВ достается ядру гелия, а 14,1 МэВ приходится на долю нейтрона. Ядро гелия полностью передает свою кинетическую энергию частицам плазмы, нагревая ее. Для нейтрона плазма практически прозрачна, он уйдет на стенку реактора.

Если за стенкой реактора поставить поглотитель нейтронов, то его энергия выделяется в виде тепла. Эту тепловую энергию можно преобразовать в электрическую с помощью водяного контура и паровой турбины или прямым преобразованием через термоэлектрические элементы.

Если предположить, что часть мощности, выделяемой с нейтронами, а также теряемая за счет излучения и тепловых потерь на стенку может быть возвращена в плазму и использована для ее подогрева, то можно найти условия, при которых реакция будет самоподдерживающейся. Это условие называется критерием Лоусона по имени английского физика, который его вывел.

Здесь n – концентрация плазмы, τ_E – время удержания тепловой энергии, T – температура плазмы.

Следовательно, для разных типов реакторов можно варьировать плотность плазмы и время удержания энергии, оставляя их произведение, удовлетворяющим критерию Лоусона.